该比赛已结束,您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。
题目描述
给定 n,m 和一棵 n 个点的有根树,1 是树根,每个点有点权,第 i 个点的权值为 ai,保证 1≤ai≤m。
定义这棵树的价值为符合以下条件的长为 m 的序列 (p1,p2,⋯,pm) 个数:
- 对每个 1≤i≤m,api=i。
- 对每个 1≤i<m,编号为 pi+1 的节点在编号为 pi 的节点的子树内。
现在有 q 次修改,第 i 次修改会将 a(i−1) mod n+1 的值修改为 vi,你需要在所有修改进行之前以及每次修改进行之后求出这棵树的价值对 109+7 取模的值。
输入格式
从文件 array.in 中读入。
第一行三个整数 n,m,q。
第二行 n−1 个整数,其中第 i 个整数为 fi+1,表示 i+1 号节点在树上的父亲是 fi+1 号节点。
第三行 n 个整数,其中第 i 个整数为 ai。
第四行 q 个整数 v1,v2,⋯,vq,vi 表示第 i 次修改会将 a(i−1) mod n+1 修改为 vi。
输出格式
输出到文件 array.out 中。
共一行 q+1 个整数,用空格隔开,其中第一个整数为初始时的答案对 109+7 取模后的结果,第 i+1 个整数为前 i 次修改后的答案对 109+7 取模后的结果。
样例 1 输入
5 2 10
1 2 1 3
1 2 2 1 1
2 2 1 2 2 2 1 2 2 2
样例 1 输出
2 0 0 0 0 1 1 2 2 2 2
样例 1 解释
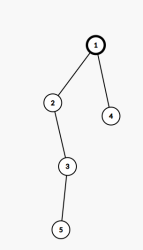
如图,初始时的 a 序列为 [1,2,2,1,1],有 [1,2],[1,3] 两种选法。
第 3 次操作后的 a 序列为 [2,2,1,1,1],没有选法。
第 7 次操作后的 a 序列为 [2,1,1,2,2],有 [2,5],[3,5] 两种选法。
样例 2∼4
见下发文件:下载链接
array2.in/ans 满足子任务 1 的限制。
array3.in/ans 满足子任务 2 的限制。
array4.in/ans 满足子任务 6 的限制。
测试点约束
对于全部测试点,$1\le n,m,q\le 5\times 10^5,1\le f_{i}<i,1\le a_i\le m$。
本题采用捆绑测试。
| 子任务编号 |
n≤ |
m≤ |
q≤ |
fi |
分值 |
| Subtask 1 |
20 |
20 |
20 |
<i |
15 |
| Subtask 2 |
400 |
400 |
400 |
<i |
20 |
| Subtask 3 |
5000 |
5000 |
5000 |
<i |
20 |
| Subtask 4 |
5×105 |
5×105 |
50 |
<i |
15 |
| Subtask 5 |
5×105 |
50 |
5×105 |
<i |
10 |
| Subtask 6 |
5×105 |
5×105 |
5×105 |
=i−1 |
10 |
| Subtask 7 |
5×105 |
5×105 |
5×105 |
<i |
10 |


 京公网安备 11011102002149号
京公网安备 11011102002149号